Sampling log-linear times

TA Trikalinos

2024-10-17

Simulation description

Assume a population of $K = 10^{5}$ individuals indexed by $k \in [K] := \{ 1, \dots, K\}$. For person $k$, we want to simulate the first occurrence of an event (e.g., emergence of a tumor) over the age (time) interval $[T_{k0}, T_{k1})$. For example, $T_{k0}$ may be the age in years when person $k$ enters the simulation, and $T_{k1}$ the age in years when that person dies from non-cancer causes. (In practice, $T_{k1}$ would be obtained by separate point process.) Only some people will develop clinical cancer over their simulated lifetime.

To fix a simulation scenario, let $a_k = 40$ for all $k$ and $b_k \sim U(50 , 100)$, where $U()$ is the uniform distribution.

We use the log-linear intensity function

$\lambda_k(t) = e^{\alpha_k + \beta_k t}$,

where $t$ is age in years. The parameters $\alpha_k, \beta_k$ are random over the individuals in the population with $\alpha_k \sim N(-4, 0.5)$, and $\beta_k \sim N_{0+}(0.03, 0.003)$, where $N()$ is a normal distribution and $N_{0+}()$ is a truncated normal distribution with support $[0, \infty)$.

Overview of sampling methods described here

We will use three methods:

1. Simulate one person at a time looping over persons. The fastest way to do this is to use a special case function in the nhppp package that samples from log-linear intensity functions in a non-vectorized fashion. Yet this will be slowest approach.

2. Simulate all persons in a vectorized way using only the intensity function $\lambda(t)$. When you only know $\lambda(t)$nhppp uses the thinning algorithm. It is a very flexible approach because it does not require a lot of information – just $\lambda(t)$. This will by much faster than the first option, but not as fast as the third option.

3. Simulate all persons in a vectorized way using the cumulative intensity function $\Lambda(t)$ and its inverse $\Lambda^{-1}(z)$, which are defined below. When you have analytic expressions for these objects, you get the fastest sampling in the nhppp package. Then the package can use the inversion or the order statistics algorithms which are more efficient.

Setup

We will use data.tables – but the same analysis should be obvious in base R. We will use functions from three more packages, without loading them: the truncnorm package is only needed for the truncated normal distribution. The tictoc() package will be used for a simple time comparison between the different ways one can simulate this problem. The stats package is used to generate normally and uniformly distributed samples.

library(data.table)
library(nhppp)

Setup pop, the population data.table. The person specific parameters $\alpha_k, \beta_k, T_{k0}$ and $T_{k1}$ are variables in pop.

pop <- setDT(
  list(
    id = 1:K,
    alpha = stats::rnorm(n = K, mean = -4, sd = 0.5),
    beta = truncnorm::rtruncnorm(n = K, mean = 0.03, sd = 0.003, a = 0, b = Inf),
    T0 = rep(40, K),
    T1 = stats::runif(n = K, min = 50, max = 100)
  )
)
setindex(pop, id)
pop
#> Index: <id>
#>             id     alpha       beta    T0       T1
#>          <int>     <num>      <num> <num>    <num>
#>      1:      1 -4.318439 0.02914304    40 74.23810
#>      2:      2 -4.200092 0.03218084    40 62.26187
#>      3:      3 -4.250369 0.02916144    40 81.29045
#>      4:      4 -4.374602 0.02269157    40 94.50129
#>      5:      5 -4.075769 0.02973159    40 67.73704
#>     ---                                           
#>  99996:  99996 -4.113622 0.03196925    40 71.34211
#>  99997:  99997 -5.111481 0.02665030    40 84.46180
#>  99998:  99998 -3.628798 0.02907565    40 87.67655
#>  99999:  99999 -4.438333 0.03027740    40 99.96851
#> 100000: 100000 -3.483592 0.02673899    40 57.45794

Intensity, cumulative intensity, and inverse cumulative intensity functions

Define some bespoke functions for the different simulation approaches below. The trick is to define functions so that they work in a vectorized form. For an example, take a look at the intensity function below. The other functions have the same bahavior.

Intensity function $\lambda()$

Define a vectorized form of the intensity function.

l <- function(t, alpha = pop$alpha, beta = pop$beta, ...) exp(alpha + beta * t)

Arguments alpha and beta can be scalars or vectors (or column matrices). Argument t can be a scalar, a vector of $K$ ages (times), or a $K \times s$ matrix. See some examples of the behavior of the vectorized function. The ellipses (...) allow l() to ignore extra arguments without breaking the execution of the script. While we won’t do that on purpose, some sampling functions in the nhppp package that take function arguments need the ability to pass optional extraneous arguments.

Scalar arguments, evaluated at t = 45

l(t = 45, alpha = -4, beta = 0.03)
#> [1] 0.07065121

Scalar arguments, evaluated at t = 45:50 (vector) or as a column matrix The function returns results in the format of the t argument.

l(t = 45:50, alpha = -4, beta = 0.03)
#> [1] 0.07065121 0.07280286 0.07502004 0.07730474 0.07965902 0.08208500

l(t = matrix(45:50, ncol = 1), alpha = -4, beta = 0.03)
#>            [,1]
#> [1,] 0.07065121
#> [2,] 0.07280286
#> [3,] 0.07502004
#> [4,] 0.07730474
#> [5,] 0.07965902
#> [6,] 0.08208500

Vector arguments, using the first 5 people and evaluating all people at t = 45

l(t = 45, alpha = pop$alpha[1:5], beta = pop$beta[1:5])
#> [1] 0.04943966 0.06380303 0.05296605 0.03496243 0.06470944

Matrix arguments are convenient: the rows are people and the columns are the ages (times) – and they can differ across persons. For the first 5 people, we evaluate a different age for each person. The results are returned in a matrix format.

l(t = matrix(c(45, 50, 45, 47.4, 30), ncol = 1), alpha = pop$alpha[1:5], beta = pop$beta[1:5])
#>            [,1]
#> [1,] 0.04943966
#> [2,] 0.07494128
#> [3,] 0.05296605
#> [4,] 0.03691928
#> [5,] 0.04142702

For the first 5 people, we evaluate three different ages for each person. We arrange a t_mat matrix of ages (times) with people in the rows and ages (times) for each person in the columns. The results are returned in a matrix format.

t_mat <- matrix(c(
  45, 50, 45, 47.4, 30,
  45.1, 50.1, 45.5, 47.8, 38,
  48, 52.7, 60.1, 70.1, 99.9
), ncol = 3, byrow = TRUE)
t_mat
#>      [,1] [,2] [,3]
#> [1,] 45.0 50.0 45.0
#> [2,] 47.4 30.0 45.1
#> [3,] 50.1 45.5 47.8
#> [4,] 38.0 48.0 52.7
#> [5,] 60.1 70.1 99.9

l(t = t_mat, alpha = pop$alpha[1:5], beta = pop$beta[1:5])
#>            [,1]       [,2]       [,3]
#> [1,] 0.04943966 0.05719509 0.04943966
#> [2,] 0.06892608 0.03937330 0.06400868
#> [3,] 0.06145926 0.05374399 0.05747231
#> [4,] 0.02982757 0.03742537 0.04163741
#> [5,] 0.10137780 0.13647889 0.33101750

The defaults for the alpha and beta arguments of the l() functions are the respective columns of the whole population. We can then evaluate the intensity function $\lambda()$ for the whole population passing only the t argument.

t_mat <- matrix(rep(c(45, 50, 55), each = K), ncol = 3, byrow = TRUE)
l(t = t_mat) |> head()
#>            [,1]       [,2]       [,3]
#> [1,] 0.04943966 0.04943966 0.04943966
#> [2,] 0.06380303 0.06380303 0.06380303
#> [3,] 0.05296605 0.05296605 0.05296605
#> [4,] 0.03496243 0.03496243 0.03496243
#> [5,] 0.06470944 0.06470944 0.06470944
#> [6,] 0.08214702 0.08214702 0.08214702

Cumulative intensity function $\Lambda(t)$

The cumulative intensity function is $\Lambda(a, t) = \int_a^t \lambda(s) \ \textrm{d}s$. It does not matter what we choose for the lower limit of integration in the definition of $\Lambda$. The lower limit cancels out in the mathematics of the sampling algorithms. Thus we are free to use any lower limit (say 0) for any antiderivative of $\lambda()$ that is convenient (for any integration constant).

With a slight abuse of notation, define 0 as the lower integration limit and write ${\Lambda(t) := \Lambda(0, t) = \int_0^t \lambda(s) \ \textrm{d}s}$. For the log-linear intensity in this example, $\Lambda(t) = \frac{1}{\beta} (e^{\alpha + \beta t} - e^\alpha)$.

The vectorized version of $\Lambda$ for our example is

L <- function(t, alpha = pop$alpha, beta = pop$beta, ...) {
  (exp(alpha + beta * t) - exp(alpha)) / beta
}

Inverse cumulative intensity function $\Lambda^{-1}(z)$

By its construction, $\Lambda$ is a strictly positive monotone function in $t$, and thus invertible. The inverse of the cumulative intensity function $\Lambda^{-1}$ is defined as the function that recovers the $t$ when you pass it the $\Lambda(t)$. The definition is that it satisfies ${\Lambda^{-1} \big ( \Lambda(t) \big ) = t}$. In our example, $\Lambda^{-1}(z) = \big(\log(\beta z + e^\alpha) - \alpha\big)/\beta$, which is easily derived from the formula of $\Lambda(t)$.

The vectorized implementation of $\Lambda^{-1}$ for our example is

Li <- function(z, alpha = pop$alpha, beta = pop$beta, ...) {
  (log(beta * z + exp(alpha)) - alpha) / beta
}

Method 1: non-vectorized sampling with nhppp::draw_sc_loglinear()

The nhppp package function draw_sc_loglinear() draws times from log-linear densities for each person at a time. This is slower than the other methods, but can be practical even for sizeable simulations that will be run once (e.g., for statistical simulation analyses) or when you develop code.

It’s arguments intercept, slope have the same name as the parameters in our log-linear intensity function $\lambda$. The t_min, t_max arguments ask for the bounds of the interval $[T_{k0}, T_{k1})$. The argument atmost1 asks only for the first time. This special case function uses a bespoke inversion algorithm; it’s as fast as we can do without vectorization.

tictoc::tic("Method 1 (nonvectorized)")
t_nonvec_special_case <- rep(NA, K)
for (k in 1:K) {
  t1 <- nhppp::draw_sc_loglinear(
    intercept = pop$alpha[k],
    slope = pop$beta[k],
    t_min = pop$T0[k],
    t_max = pop$T1[k],
    atmost1 = TRUE
  )
  if (length(t1) != 0) {
    t_nonvec_special_case[k] <- t1
  }
}
tictoc::toc(log = TRUE)
#> Method 1 (nonvectorized): 1.498 sec elapsed
pop[, t_nonvec_special_case := t_nonvec_special_case]

Method 2: Vectorized sampling using only $\lambda()$

When you only know the intensity function $\lambda$, nhppp employs a thinning algorithm.

One of the items needed for the thinning algorithm is a piecewise constant majorizer function $\lambda_*$ such that: $\lambda_*(t) >= \lambda(t)$ for all $t$ of interest.

The nhppp::vdraw_intensity function assumes that you will provide the majorizer function as a matrix (lambda_maj_matrix). To create this matrix, split the simulation time (here, from age 40 to age 100) in $M$ equal-length intervals. For person $k$ and interval $m$, the element lambda_maj_matrix[k, m] records a supremum of $\lambda_k$ over the $m$-th interval. Any supremum will do – but the algorithm is most efficient when you give it the least upper bound – practically, the maximum of $\lambda(t)$ over all $t$ in the interval. For monotone intensity functions, such as the function in the example, the maximum is at one of the interval’s bounds. It will be at the left bound, if $\lambda$ is decreasing, and at the right bound, if $\lambda$ is increasing.

There is a helper function in nhppp that generates the majorizer matrix automatically for monotone (and possibly discontinuous) functions and for nonmonotone continuous Lipschitz functions (functions whose maximum slope is bounded). Even if your case is more complex, you should be able to find a supremum that works.

This code samples in a vectorized fashion when you know only $\lambda()$. It creates a majorizer matrix over $M=5$ intervals. To let the software know which times correspond to each of the $M$ intervals it suffices to specify a start and stop time for each row of the majorizer matrix with the rate_matrix_t_min and rate_matrix_t_max options. The sampling intervals $[T_{k0}, T_{k1})$for each simulated person are a subset of the interval for which the majorizer matrix is defined, and are specified with the t_min and t_max options. (The atmostB option can be useful to speed up the sampling and minimize memory needs when one is interested in the first event only. The smaller the value, the faster the algorithm but you have to check that you have not specified it to be too small. In this example, atmostB = 5 is fine – it returns exact solutions; but we have checked it [not shown]. If you do not want to mess with it, do not use the option. The function may be already fast enough for your needs).

tictoc::tic("Method 2 (vectorized, thinning)")
M <- 5
break_points <- seq.int(from = 40, to = 100, length.out = M + 1)
breaks_mat <- matrix(rep(break_points, each = K), nrow = K)

lmaj_mat <- nhppp::get_step_majorizer(
  fun = l,
  breaks = breaks_mat,
  is_monotone = TRUE
)

pop[
  ,
  t_thinning := nhppp::vdraw_intensity(
    lambda = l,
    lambda_maj_matrix = lmaj_mat,
    rate_matrix_t_min = 40,
    rate_matrix_t_max = 100,
    t_min = pop$T0,
    t_max = pop$T1,
    atmost1 = TRUE,
    atmostB = 5
  )
]
tictoc::toc(log = TRUE) # timer end
#> Method 2 (vectorized, thinning): 0.11 sec elapsed

Method 3: Vectorized sampling using $\Lambda()$ and $\Lambda^{-1}()$

The most efficient sampling is possible when one knows $\Lambda()$ and $\Lambda^{-1}()$. The nhppp package can sample in this case using the vdraw_cumulative_intensity() function. Here range_t is a matrix with information on each person’s $[T_{k0}, T_{k1})$.

tictoc::tic("Method 3 (inversion)")
pop[
  ,
  t_inversion := nhppp::vdraw_cumulative_intensity(
    Lambda = L,
    Lambda_inv = Li,
    t_min = pop$T0,
    t_max = pop$T1,
    atmost1 = TRUE
  )
]
tictoc::toc(log = TRUE) # timer end
#> Method 3 (inversion): 0.016 sec elapsed

Comparisons

Simulation time-costs

The simulation time-costs that you see in this document depend on the machine that rendered it. If you read this online, this machine is probably some virtual server with minimal resources. If you installed the package locally, it is probably the machine you are using to run R.

1. Method 1 (nonvectorized): 1.498 sec elapsed. This is the slowest approach – but still not bad for $10^{5}$ samples!

2. Method 2 (vectorized, thinning): 0.11 sec elapsed. This approach is many times faster that then first approach. It is very flexible – it can accommodate very complex time varying intensity functions. You almost always know $\lambda$ and can get its majorizer $\lambda_*$ easily and fast.

3. Method 3 (inversion): 0.016 sec elapsed. This approach is many times faster that the second one, but requires implementations for $\Lambda$ and $\Lambda^{-1}$.

Simulated times

All three methods sample correctly from the specified log-linear process. There is no approximation at play.

The QQ plots compare the simulated times with the three methods. The agreement is excellent over this population of size $K = 10^{5}$. As $K$ increases the agreement remains excellent (not shown here - try it for yourself). The paper in the bibliography includes in-depth comparisons. A set of QQ plots should suffice here.

qqplot(pop$t_nonvec_special_case, pop$t_thinning)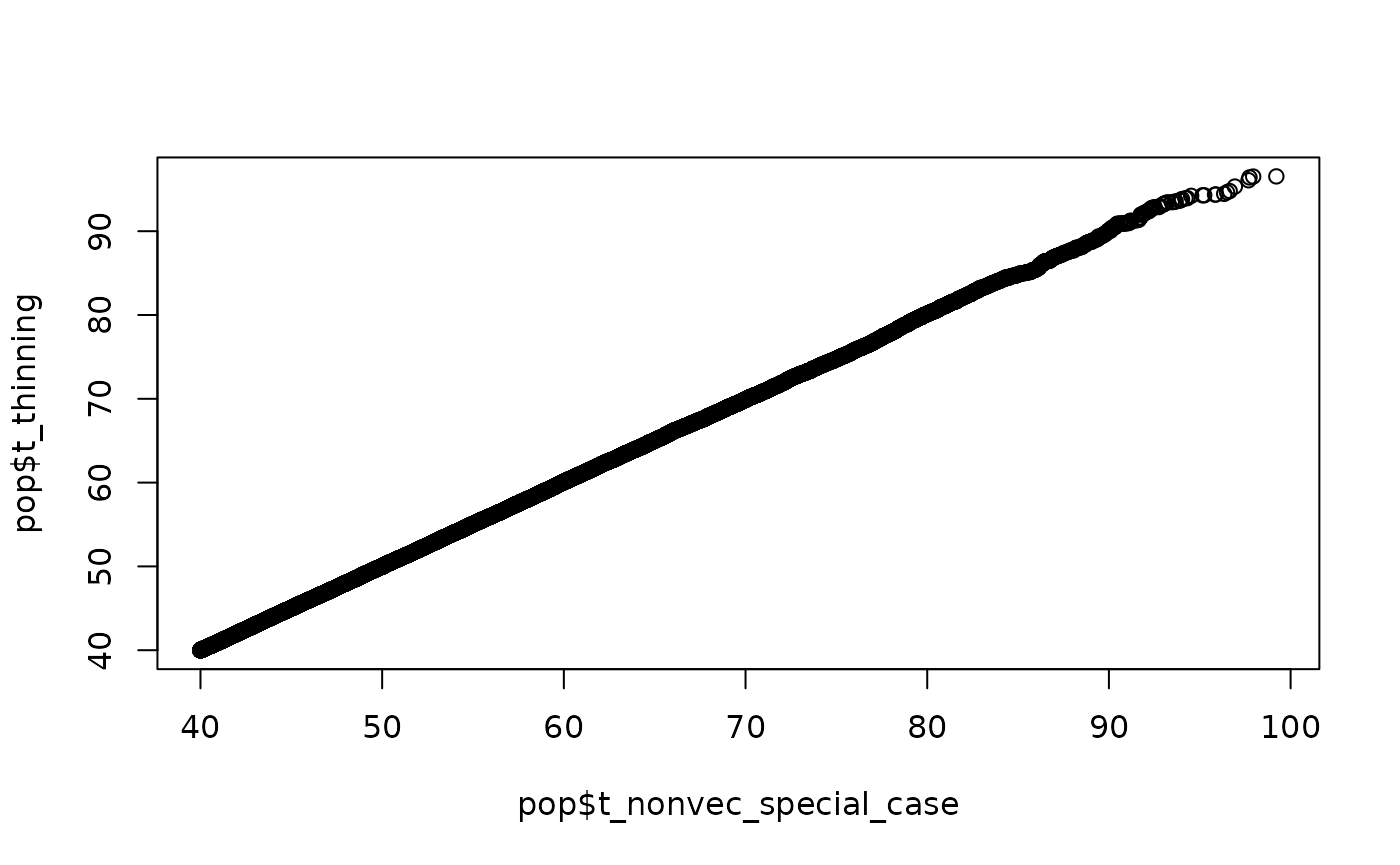

qqplot(pop$t_nonvec_special_case, pop$t_inversion)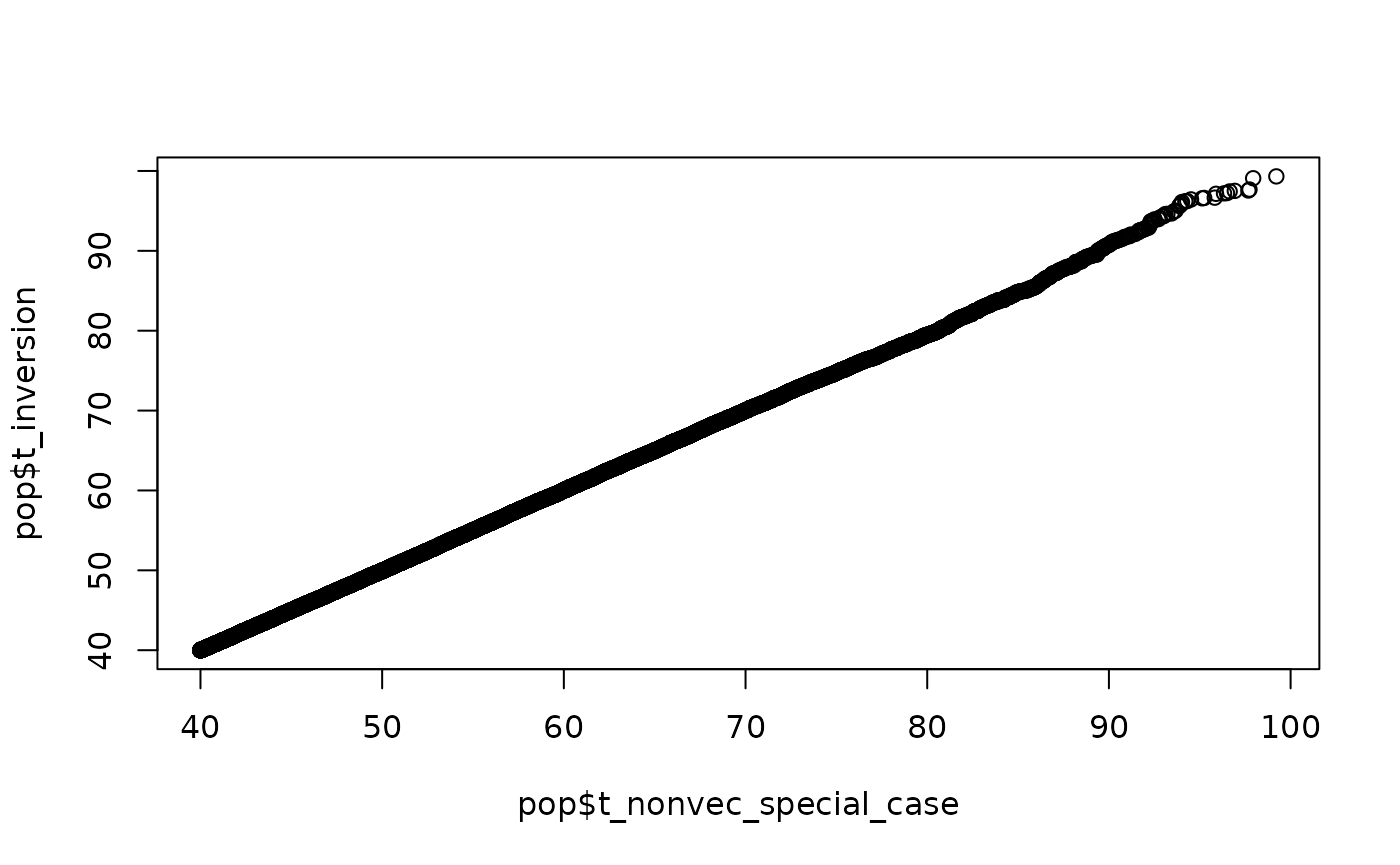

Acknowledgments

Thanks to Carolyn Rutter and Hui Hsuan Chan for providing the numerical example in this vignette.

Bibliography

Trikalinos TA, Sereda Y. nhppp: Simulating Nonhomogeneous Poisson Point Processes in R. arXiv preprint arXiv:2402.00358. 2024 Feb 1.

Since the publication of the paper, the syntax and options of the nhppp package have evolved. To reproduce the code in the paper, you have to install the version of nhppp used in the paper. Alternatively, take a look at the vignettes, which are written to work with the current package.